مدل های برنامه نویسی در رایانش ابری

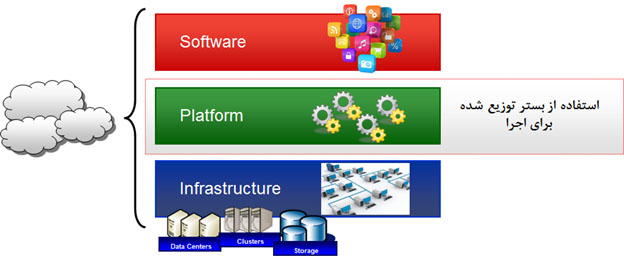
رايانش ابري داراي يک معماري سه لايه است که در لايه زيرساخت با مديريت منابع مواجه هستيم، در لايه بستر امکاناتي براي توسعه برنامه‌هاي کاربردي بر روي منابع ابري فراهم شده است و در لايه نرم‌افزار، برنامه¬هاي کاربردي براي استفاده توسط کاربر نهايي قرار مي¬گيرد. معماري در شکل زیر نشان داده شده است.

معماري سه لايه رایانش ابری و نقش لایه پلت فرم

در هنگام استفاده از بسترهای رایانش ابری، کاربر نیازی به درگیر شدن در جزئیات فنی و زیرساخت ابر ندارد، بلکه تنها کافیست روی خودِ برنامه متمرکز شود. مدل های برنامه نویسی ارائه شده در بسترهای رایانش ابری به کاربر کمک میکنند تا بدون درگیر شدن در جزئیات فنی، با رعایت یک سری قواعد، برنامه خود را بگونه ای بنویسند که قابلیت اجرا در داخل ابر را داشته باشد. برای مثال با استفاده از مدل نگاشت کاهش، در واقع کاربر تنها کافیست توابع نگاشت و کاهش را بنویسد و جزئیات ابر و منابع از دید او پنهان است. وظیفه لایه¬ی پلت فرم این است که توابع و داده¬های کاربر را بگیرد، بر اساس منابعی که در اختیار دارد، داده را روی گره¬ها توزیع کند و تابع نگاشت را روی تعداد گره¬ی مورد نیاز زمانبندی و اجرا کند، سپس با زمانبندی و اجرای تعدادِ مورد نیاز از تابع کاهش، خروجی¬ها را به تابع کاهش تحویل دهد و نتیجه نهایی را روی دیسک قرار دهد.

با این حال اجرای برنامه ها لزوما بهینه نخواهد بود و برنامه نویس میبایست با شناخت دقیق محیط اجرا و چهارچوب ارائه شده در مدل برنامه نویسی، بتواند حداکثر سازگاری جهت اجرای برنامه مورد نظر در بسترهای ابری را ایجاد کند. پارامترهای بسیاری نظیر تکرار داده، ساختار ذخیره سازی داده، نحوه توزیع پردازش، نحوه ایجاد واحدهای پردازشی، میزان اطلاعاتی که باید مبادله شود، هزینه محاسبات داخل هر نود نسبت به ارتباطات بین نودها، میزان سازگاری الگوریتم ها و مدل برنامه با محیط توزیع شده، انتخاب صحیح شاخص های ارزیابی کارهایی، شناسایی گلوگاهها، شناسایی تغییرات ایجاد شده در الگوریتم، تاثیر میزان توزیع شدگی و ساختار آن در رفتار الگوریتم و ... از جمله چالش های پیش رو برای اجرای برنامه ها در بسترهای ابری می باشد.

مدل نگاشت-کاهش

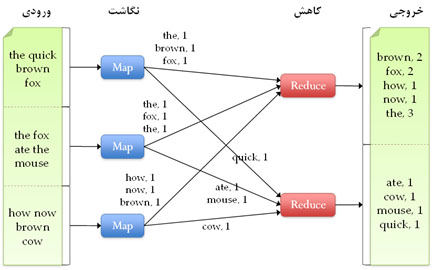
بطور خلاصه مدل نگاهش-کاهش يک روش برنامه نويسي رايج در سيستم¬هاي توزيع شده نظير رايانش ابري است که مي¬تواند راهکارهايي را براي حل مسئله با يک شيوه تفکر متفاوت بر روي مسئله ارائه دهد. مسائلي که بصورت نگاشت-کاهش حل مي¬شوند بايد قابليت تقسيم پذيري داشته باشند. در اين روش پردازش به دو مرحله اصلي تقسيم مي¬شود. در مرحله نگاشت، مجموعه داده به مقدار مورد نياز تقسيم شده و به نودهاي مختلف ارسال مي¬گردد و بخشي از محاسبات در آنها صورت مي¬گيرد. نتيجه محاسبات به نودهاي کاهش دهنده ارسال مي،شوند که وظيفه جمع بندي و ارائه نتايج نهايي را دارند. به عنوان يک مثال رايج، براي شمارش سريع کلمات يک مجموعه فايل ورودي، مي¬توان هر فايل را به يک نود نگاشت ارسال کرد که کلمات مربوط به فايل خود را شمارش کند، سپس هر دسته از کلمات براييک کاهش دهنده ارسال گردد تا جمع نهايي هر کلمه را حساب کند. اين مثال در شکل زیر نشان داده شده است.

شناخت شيوه تفکر با استفاده از مدل نگاشت-کاهش براي حل مسئله به کمک آن بسيار مهم است، بنابراين کمي بيشتر روي مثال شمارش کلمات تمرکز مي¬کنيم تا سپس بتوان به مسئله اصلي پرداخت. تابع نگاشت در مثال شمارش کلمات مي¬تواند خيلي ساده و بصورت زير تعريف شود:

map(String key, String value){
	for each word in value:
		SendtoReducer(word,”1”); 
}

در زمان اجرا، به ازاي هر خط از فايل ورودي تابع نگاشت فوق فراخواني مي¬شود. محتوا در متغيير value قرار دارد. متغيير key در اينجا قابل صرف نظر کردن است. اين تابع کلمات را جدا مي¬کند و به ازاي هر کلمه، اعلام مي¬کند که يک بار آن را ديده است. مجموعه نتايج پيش از ارسال شدن به تابع کاهش، مرتب سازي شده و تابع کاهش به ازاي هر مجموعه با يک کليد يکسان فراخواني مي¬شود. بنابراين تابع کاهش مي¬تواند بصورت زير نوشته شود.

reducer(String key, Iterator values){
int result=0;
	for each v in values:
result += v;
	Print(key + “:” + result);
}

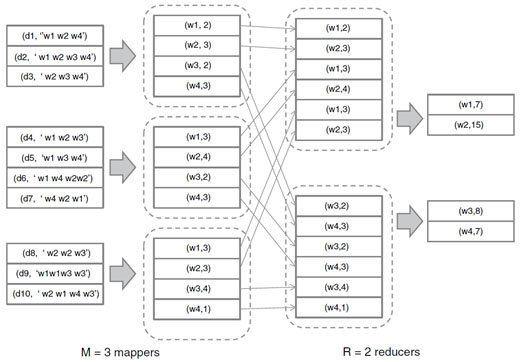
اين مثال با يک شيوه نمايش ديگر بصورت کامل¬تر در شکل زیر ارائه شده است که مثلا در هر کاهش دهنده مي¬توان يک بار مجموع کلماتي که مشاهده کرده است را نيز محاسبه کرد (توسط يک تابع شبيه کاهش که بصورت محلي در همان نود اجرا مي شود) و سپس نتيجه را به کاهش دهنده¬هاي اصلي ارسال کرد.

Map:  (k1, v1) -> [(k2, v2)].
Reduce: (k2, [v2]) -> (k2, f([v2])).

لازم به ذکر است که کارهاي مياني که بين تابع نگاشت و کاهش انجام مي¬شود (نظير مرتب سازي داده هاي مياني و چگونگي توزيع آنها به نودهاي کاهش دهنده) توسط خود بستر اجرا صورت مي¬گيرد و در صورت نياز به بهينه سازي بيشتر مي-توان به آن توابع نيز دسترسي داشت.

استفاده از مدل نگاشت کاهش برای حل مسائل در حوزه الگوريتم های تکاملی

اجراي برخی مسائل در حوزه الگوریتم های تکاملی با استفاده از مدل نگاشت-کاهش، داراي ملاحظات و پيچيدگي هاي بسياري است که عمده¬ترين آنها که باعث افزايش پيچيدگي مسئله مي¬شود، وجود اطلاعاتي است که بصورت متاديتا بايد بين نودها بصورت مشترک وجود داشته باشد و نيز اطلاعاتي وجود دارد که بايد در هر بار تکرار حفظ شود. مدل پايه نگاشت کاهش از اين نيازمندي¬ها پشتيباني نمي¬کند. اين مشکلات با جزئيات بيشتر پس از شرح سطح بالاي راهکارهاي ارائه شده براي اجراي مسئله مورد بررسي قرار خواهد گرفت.

تکرار جمعيت¬هاي پدر

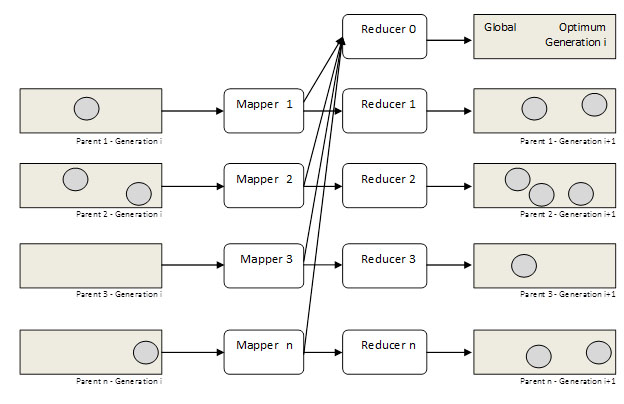
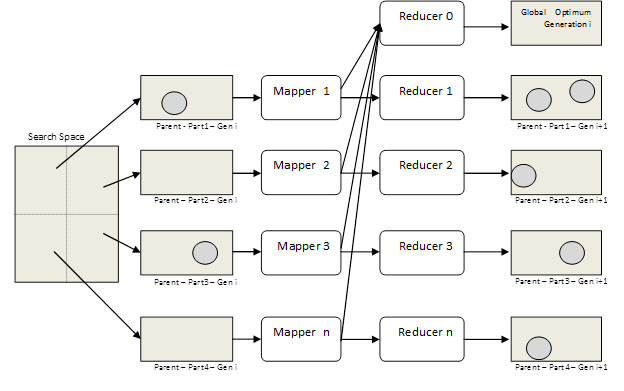
يک شيوه اوليه براي حل مسئله اين است که همزمان چندين جمعيت پدر داشته باشيم که هر کدام به يکي از نود نگاشت ارسال شوند. پس از انجام محاسبات مربوط به شايستگي و محاسبه بهينه محلي در هر جمعيت در هر نود نگاشت، نتايج به نود کاهش متناظر ارسال مي گردد تا عمليات بازترکيبي، جهش، و محاسبات مربوط به جمعيت¬هاي فرزند در آن صورت گيرد. بهينه محلي هر يک از نگاشت¬ها به کاهش¬دهنده صفر ارسال مي¬شود تا بهينه عمومي آن نسل را حساب کند. اين فرآيند براي نسل بعد تکرار مي شود. در اين روش مشکل متاديتا به حداقل مي¬رسد، زيرا فقط بايد اطلاعات مربوط به جمعيت¬هاي فرزند را در هر بار تکرار براي هر جمعيت حفظ کنيم.

در اين روش، با هر جمعيت پدر بصورت مستقل از ساير جمعيت¬ها رفتار مي¬شود و مقياس پذيري بالايي در خصوص اجراي همزمان تعداد زيادي جمعيت پدر دارد، اما مقياس پذيري آن براي افزايش مقياس خود مسئله پايين است. زيرا اگر اندازه مسئله و فضاي جمعيت بزرگ شود، هر نسخه از مسئله بايد در يکي از نودها بطور کامل اجرا شود. البته اگر اندازه جمعيت را زياد نکنيم و تنها فضاي مسئله بزرگ شود، همچنان انتظار مي¬رود که اجراي موازي چندين جمعيت بتواند نسبت به يک جمعيت موثرتر باشد. اين موضوع در بستر رايانش ابري که منابعي در سطح مراکز داده در اختيار کاربر قرار مي¬دهد بسيار قابل توجه است، زيرا مي¬توان همزمان هزاران نود را براي انجام چنين محاسباتي بکار گرفت. براي افزايش انعطاف پذيري روش جهت حل مسائل با مقياس بزرگتر که از توان يک سيستم خارج است، راهکار ديگري پيشنهاد شده است که در ادامه ارائه شده است.

تقسيم فضاي مسئله

راهکار تقسيم فضاي مسئله، براي افزايش توانايي روش ارائه شده جهت حل مسائل با مقياس بزرگتر ارائه شده است که البته جزئيات و پيچيدگي¬هاي بيشتري دارد. همانطور که مشاهده مي¬شود، فضاي مسئله بگونه¬اي شکسته مي¬شود که نود بتواند فضاي محدودي را جستجو کند. انتظار مي¬رود با افزايش تعداد نودها، جواب¬هاي بهينه در زمان کوتاه¬تري بدست آيد، ضمن اينکه با افزايش فضاي مسئله، يک سيستم واحد قادر به حل مسئله نيست، اين راهکار مي¬تواند از عهده چنين مسائلي نيز برآيد.

نکته¬اي که اينجا وجود دارد اين است که بايد علاوه بر اطلاعات مربوط به جمعيت¬هاي فرزند، اطلاعات مربوط به هر يک از فضاهاي جستجو نيز حفظ شود و به نسل بعد منتقل شد. لازم به ذکر است که جمعيت هاي فرزند در همان نودهايي پردازش مي¬شوند که جمعيت پدر وجود دارد. براي بهبود راه حل و پيدا کردن نقاطي که ممکن است در قسمت هاي لبه يا گوشه قرار داشته باشند، مي¬توان درصدي همپوشاني بين فضاهاي جستجو قرار داد. همچنين بايد در نظر داشت که در صورت افزايش ابعاد مسئله، تعداد نودهاي مورد نياز بصورت نمايي افزايش مي¬يابد. مثلا براي دو بعد (d=2) و تقسيم هر بعد به دو قسمت (p=2) تعداد نودهاي مورد نياز چهار عدد خواهد بود (N=4) که مي¬توان آن را بصورت رابطه زير بيان کرد:

N = p ^ d

همچنين بايد يک رابطه جهت تبديل مختصات فضاي تقسيم شده به شماره نود مورد نظر در نظر گرفته شود که براي دو بعد بصورت part_num = i * p + j + 1 مي¬باشد. در صورتي که بخواهيم مقياس را بازهم افزايش دهيم، مي¬توان از راه کاري ديگري که در ادامه آمده است استفاده نمود که بيشترين پيچيدگي را دارد.